type
status
date
slug
summary
tags
category
icon
password
Email
三种寻路算法
- A星寻路算法(常用):一定能找到最短路径,可以走直线和斜线,而且开销较小,常用于大型地图的寻路
A星寻路算法
A星寻路算法思想
引入: 狼吃羊模型。狼捕猎羊:如果抓到了就加100分;如果狼不动,每分钟减2分;如果狼抓捕时会跑,跑步每分钟减5分;狼会饿 ,饿的时候每分钟减10分。 有一个积分的概念在这里面。结果会发现狼会站在原地不动。因为狼直到,抓住羊很困难,跑步时会扣分,饿时会扣分,不动时也会扣分。但是人工智能狼计算出了站着不动时扣分的代价最低,而干其他事代价都高,因此狼会自动选择代价最低的方式,一动不动之后又加了设定:原地不动每分钟也扣分,而且是线性扣分。结果你会发现狼从一开始就会自杀。同理,自杀是代价最小的选择(即分数最高,如果你干其他的事,则可能会负分,所以狼会选择自杀)。
A星寻路算法也引入了这一概念,即通过计算和量化行走的各个方向的代价,来选择最优路径
- 公式: f = g + h
- f: 设定其为最终评估代价
- g:当前点走到下一点的付出的代价
- h:当前点到终点的预期代价
- 通过比较各条路线的最终代价,选择最小代价,即为合适的路径,也为最短路径。
A星寻路准备
- 记录坐标点的类型,GetH和GetF函数即为计算各种代价的函数,稍后会介绍。一个重载用来比较当前点是否到达终点
h表示当前点到终点的预期代价,因此我们每次移动一步,都需要求出 h,而h的计算我们可以直接通过数格子来获得,即水平,竖直个有几个格子,这便是预期的代价 g表示走到每一点的代价,因此每走一个方向,记录这个方向的代价, 最后选择代价最小的方向即可,g可以通过遍历八个方向来记录 f =g + h
- 存储位置节点的树结构,含有构造函数用来构建树节点,vector数组存储多个节点:因为一个父亲会有多个孩子的情况。
- 判断是否能走的函数,用于判断地图某个点是否能走,即不为墙,没越界,没走过,则能走。
- 数据的准备
- 起点与终点的坐标
- 树根节点,用于保存寻路的树结构
- buff数组来记录每一个孩子节点,用来确定下一步该走的点
- vis标记数组,不能重复走
- 当前点与试探点
A星寻路过程(图例)
假定直着走的代价为10,斜着走的代价为14
- 首先计算起点位置周围八个方向付出代价(蓝色),此代价为付出的代价 g。

- 然后再计算起点到终点的代价(如何计算:数格子即可,某个点到终点的格子数,只能行列,不能斜着),此代价为预期代价h,可以发现 最终代价=付出+预期,可以得到一个最小的代价点,即右下角的斜着的点。
这个点即是我们下一步要走的点。依次类推,在下个点上,再次计算周围代价最小的点,然后再次移动
upd: 2023. 2.22 新增一个图

- 注意:标记起始点和每个移动到的点为已经走过点,即下一次不会重复移动到这个点。
- 在移动到的点处(代价最小点),继续遍历八个方向,除了墙壁和已经走过点,继续计算最终代价,找到最终代价小的点,移动。

- 注意:如果你移动到了一个死胡同,则必须回退,如何回退? 我们事先准备了一个容器vector名字叫做 buff ,来存储我们每次遍历的方向的节点,即我们把每一个方向都创建一个节点,然后节点入树,节点再入容器,当我们走到死胡同时,通过找到容器内的最小元素(即是代价最小点,但是这个点是死胡同),然后把他删除,则 ==再次找一个代价最小点,然后移动到它那里去== 。 如果地图没有终点,则可以想到,容器会一直删除,然后为空,此时则退出,没有终点。
A星寻路代码(完整)
终点row,col(7,7):

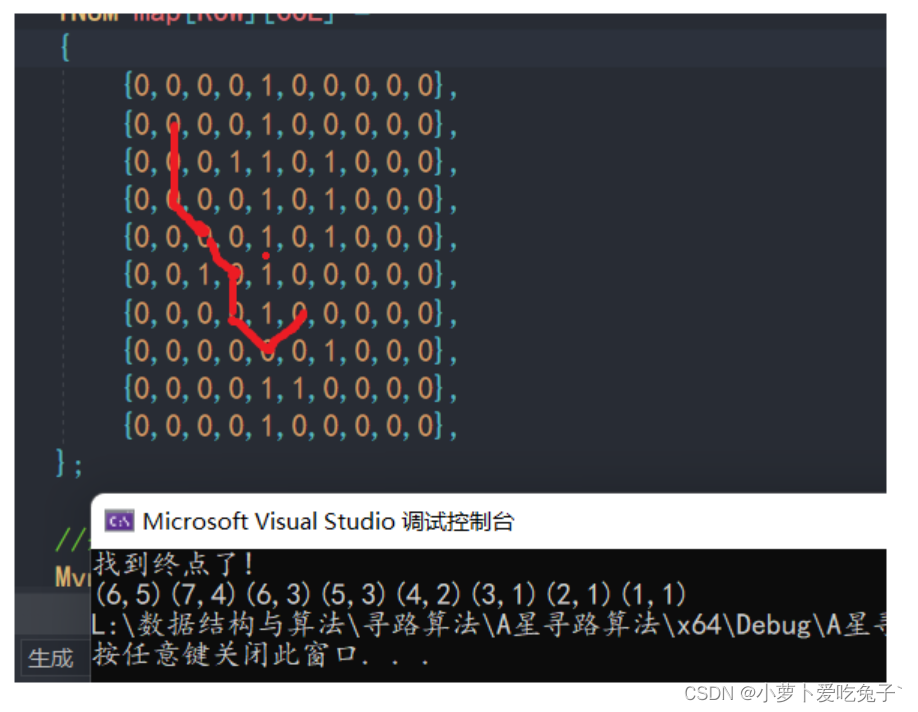
终点row,col(6,5)
- 作者:Yuleo
- 链接:https://www.helloylh.com/article/6d186eda-0edc-4970-9d3b-c580ff2a37a0
- 声明:本文采用 CC BY-NC-SA 4.0 许可协议,转载请注明出处。