type
status
date
slug
summary
tags
category
icon
password
Email
文章首发于:My Blog 欢迎大佬们前来逛逛
字典树(Trie树)
一:概念
字典树是一种树形结构,用于存储一组字符串,支持快速的字符串查找和前缀匹配。
字典树的本质是利用字符串之间的公共前缀,将具有相同前缀的字符串合并在一起,从而实现高效的字符串操作。
数据结构 字典树是一棵多叉树,每个节点包含若干个指向子节点的指针,每个节点代表一个字符。根节点代表空字符串,每个非根节点代表一个非空前缀。如果某个节点代表的字符串在字典树中存在,则该节点为终止节点;否则,该节点不是终止节点。
三:操作
字典树支持以下操作:
- 插入操作: 将一个字符串插入字典树中,需要从根节点开始遍历字符串的每个字符,如果当前字符对应的节点存在,则继续向下遍历;否则,新建一个节点,并将其插入到当前节点的子节点中。最后,将字符串的最后一个字符对应的节点标记为终止节点。
- 查找操作: 查找一个字符串是否在字典树中,需要从根节点开始遍历字符串的每个字符,如果当前字符对应的节点存在,则继续向下遍历;否则,说明该字符串不存在于字典树中。
- 前缀匹配操作:在字典树中查找一个字符串的前缀匹配,需要从根节点开始遍历字符串的每个字符,如果当前字符对应的节点存在,则继续向下遍历;否则,说明该字符串的前缀不存在于字典树中
四:应用场景
字典树的应用场景非常广泛,包括但不限于以下几个方面:
- 字符串查找:在一组字符串中查找指定的字符串是否存在,可以使用字典树来实现。
- 词频统计:将一组文本分词,并统计每个词出现的频率,可以使用字典树来实现。
- 自动补全:在用户输入过程中,根据已输入的前缀,自动补全可能的后缀,可以使用字典树来实现。
- 模式匹配:在一组文本中查找某个模式出现的位置,可以使用字典树来实现。
143. 最大异或对
题目要求:给你一些数字,让你找出其中异或和最大的一对数字
示例:
其中 2和5 或者 4和3异或和之后为7,都是最大值,因此结果为7.
如果我们知道一个数字比如 4,则此二进制为 100,则我们尽量需要找 011的,因为只有这样我们的异或和是 111,是一个在这两个数字异或范围内的最大值。
同理,对于其他的数字也是,我们只要找到与num每一位二进制数尽量相反的数字即可
因此对于所有的数字都是如此,最大的数字可以到达 2^31,所以我们在对Trie树进行操作的时候要:
其中~i表示 i>=0,两者等价
过程如下:
- 对于每一个数字进行插入到字典树中。
- 对于每一个数字在Trie中查询其最大异或值。
- 最后输出最大值。
Trie图如下所示:
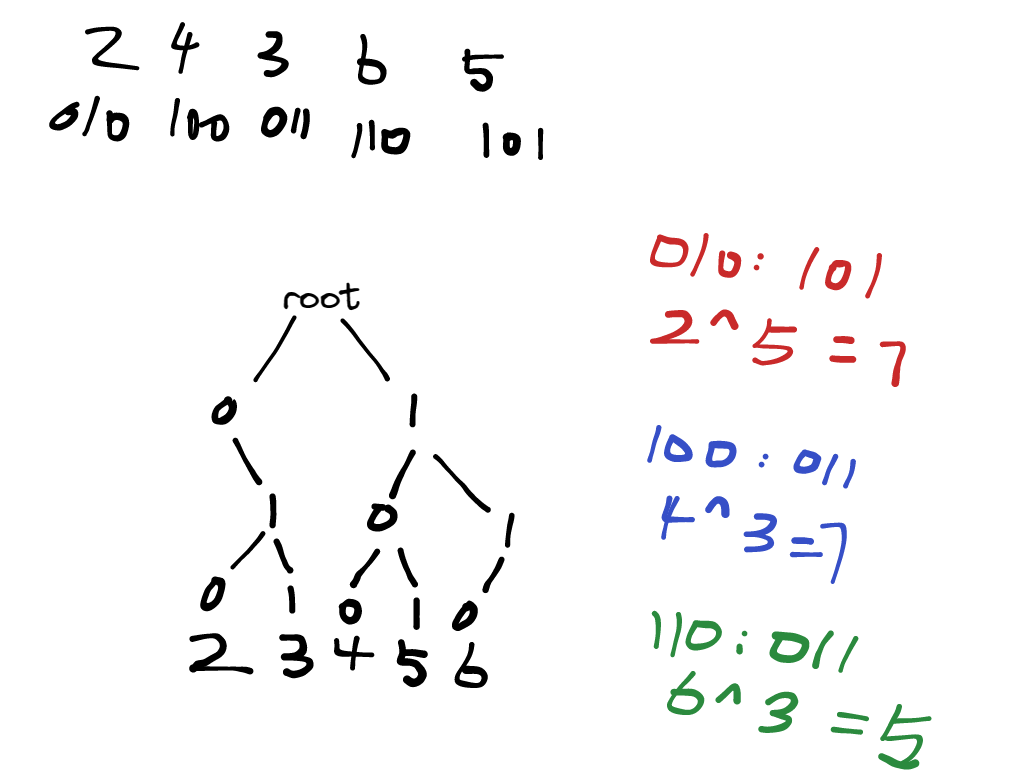
因此我们插入之后形成的Trie树如上图所示。
对于查询每一对之间的最大异或值,我们首先要尽量找到每一位都与当前数字相反的Trie分支;如果没有与当前数字相反的分支,则我们只能选择与当前数字相同的分支。
- 如何获取当前数字的每一个位数?
- 如何以当前数字的二进制位的数值创建Trie分支?
- 查询时如何当前二进制位有没有相同的分支?
完整代码如下:
3485. 最大异或和
题目要求:找到序列中长度不超过m的子序列的最大异或值和。
最大异或对与这道题相似,只不过这道题求得是不超过m的子序列的最大异或和。
首先我们需要知道几个性质:
- 前缀和不仅可以维护和,还可以维护异或值的和。
因此 sum[i]-sum[j-1] 表示 【j,i】范围内的数字的异或和
因此对于一个长度不超过M的子序列来说,如果我们固定住右端点 i ,则我们就可以枚举左端点 j。
通过sum[i]-sum[j-1],如果sum[i]是固定的,则 j 就可以通过在 [ i-M+1,i ] 中找到最小的异或值的和,即寻找sum[j-1]的最小值
再通过sum[i] -sum[j-1]得到长度不超过m的子区间[j,r]的异或和的最大值。
因此我们就需要维护一个窗口,同时需要完成以下三种操作:
- 往区间中插入元素(窗口右端点)。
- 往区间中删除元素(窗口左端点的前一个位置)。
- 找到与sum[i]异或值最大的数。
通过query函数便可以找到与 sum[i]异或值和最大的结果。
最后ans就是我们的答案。
其中我们需要注意由于需要维护一个长度为M的窗口,因此当我们需要在移动的时候删除窗口左端点元素,与添加一个元素到右端点。
- 何时删除元素?
由于 j 属于 [i-M+1,i]中, 因此 j-1 属于 [i-M,i-1]中,因为对于前缀和我们需要的是 sum[j-1]。因此 i - M表示的是长度为M窗口需要求前缀和的最左端位置,因此窗口往右移动的时候,我们需要删除最左端位置的前一个位置:
- 何时插入元素?
枚举新的右端点 i ,直接插入即可:
要时刻记住:我们都是对
某个区间异或和的前缀和 进行操作的,而不是原数组,不要搞混了。- 作者:Yuleo
- 链接:https://www.helloylh.com/article/00ef9387-5f4f-4527-bfad-e636790f8be2
- 声明:本文采用 CC BY-NC-SA 4.0 许可协议,转载请注明出处。